Fight Finance

For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.

For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.

For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.

For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.

For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.

A three year bond has a face value of $100, a yield of 10% and a fixed coupon rate of 5%, paid semi-annually. What is its price?

A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.

The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.

Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?

A European company just issued two bonds, a

• 2 year zero coupon bond at a yield of 8% pa, and a
• 3 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.

Which bond would have the higher current price?

A European company just issued two bonds, a

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?

The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.

Considering this, which of the following statements is NOT correct?

A two year Government bond has a face value of $100, a yield of 2.5% pa and a fixed coupon rate of 0.5% pa, paid semi-annually. What is its price?

Which of the following statements about risk free government bonds is NOT correct?

Hint: Total return can be broken into income and capital returns as follows:

###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###

The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.

The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.

Considering this, which of the following statements is NOT correct?

An Australian company just issued two bonds paying semi-annual coupons:

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

An Australian company just issued two bonds:

• A 1 year zero coupon bond at a yield of 10% pa, and
• A 2 year zero coupon bond at a yield of 8% pa.

What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?

Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?

An Australian company just issued two bonds:

• A 6-month zero coupon bond at a yield of 6% pa, and
• A 12 month zero coupon bond at a yield of 7% pa.

What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100) and maturity (3 years).

The only difference is that bond X and Y's yields are 8 and 12% pa respectively. Which of the following statements is true?

A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?

Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.

Which of the following statements is true?

A four year bond has a face value of $100, a yield of 6% and a fixed coupon rate of 12%, paid semi-annually. What is its price?

Which one of the following bonds is trading at a discount?

A firm wishes to raise $20 million now. They will issue 8% pa semi-annual coupon bonds that will mature in 5 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

A five year bond has a face value of $100, a yield of 12% and a fixed coupon rate of 6%, paid semi-annually.

What is the bond's price?

Which one of the following bonds is trading at par?

A firm wishes to raise $8 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?

Let: ##P_0## be the bond price now,

##F_T## be the bond's face value,

##T## be the bond's maturity in years,

##r_\text{total}## be the bond's total yield,

##r_\text{income}## be the bond's income yield,

##r_\text{capital}## be the bond's capital yield, and

##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.

The coupon rate of a fixed annual-coupon bond is constant (always the same).

What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:

###r_\text{total} = r_\text{income} + r_\text{capital}###

###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###

Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.

Select the most correct statement.

From its date of issue until maturity, the income return of a fixed annual coupon:

Which one of the following bonds is trading at a premium?

An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.

A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.

A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue? All numbers are rounded up.

A four year bond has a face value of $100, a yield of 9% and a fixed coupon rate of 6%, paid semi-annually. What is its price?

In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.

A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?

A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?

Bonds X and Y are issued by the same company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X pays coupons of 6% pa and bond Y pays coupons of 8% pa. Which of the following statements is true?

A 30 year Japanese government bond was just issued at par with a yield of 1.7% pa. The fixed coupon payments are semi-annual. The bond has a face value of $100.

Six months later, just after the first coupon is paid, the yield of the bond increases to 2% pa. What is the bond's new price?

A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.

Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?

Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?

Economic statistics released this morning were a surprise: they show a strong chance of consumer price inflation (CPI) reaching 5% pa over the next 2 years.

This is much higher than the previous forecast of 3% pa.

A vanilla fixed-coupon 2-year risk-free government bond was issued at par this morning, just before the economic news was released.

What is the expected change in bond price after the economic news this morning, and in the next 2 years? Assume that:

• Inflation remains at 5% over the next 2 years.
• Investors demand a constant real bond yield.
• The bond price falls by the (after-tax) value of the coupon the night before the ex-coupon date, as in real life.

Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.

Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.

Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.

Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid semi-annually. So there are two coupons per year, paid in arrears every six months.

The expression 'my word is my bond' is often used in everyday language to make a serious promise.

Why do you think this expression uses the metaphor of a bond rather than a share?

Risk-free government bonds that have coupon rates greater than their yields:

A 'fully amortising' loan can also be called a:

A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 3 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.

Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.

What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?

An investor bought a 20 year 5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.

Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly rose to 5.5% pa. Note that all yields above are given as APR's compounding semi-annually.

What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?

In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:

###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###

Which of the following statements is NOT correct?

In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:

###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###

Which of the following statements is NOT correct?

On 22-Mar-2013 the Australian Government issued series TB139 treasury bonds with a combined face value $23.4m, listed on the ASX with ticker code GSBG25.

The bonds mature on 21-Apr-2025, the fixed coupon rate is 3.25% pa and coupons are paid semi-annually on the 21st of April and October of each year. Each bond's face value is $1,000.

At market close on Friday 11-Sep-2015 the bonds' yield was 2.736% pa.

At market close on Monday 14-Sep-2015 the bonds' yield was 2.701% pa. Both yields are given as annualised percentage rates (APR's) compounding every 6 months. For convenience, assume 183 days in 6 months and 366 days in a year.

What was the historical total return over those 3 calendar days between Friday 11-Sep-2015 and Monday 14-Sep-2015?

There are 183 calendar days from market close on the last coupon 21-Apr-2015 to the market close of the next coupon date on 21-Oct-2015.

Between the market close times from 21-Apr-2015 to 11-Sep-2015 there are 143 calendar days. From 21-Apr-2015 to 14-Sep-2015 there are 146 calendar days.

From 14-Sep-2015 there were 20 coupons remaining to be paid including the next one on 21-Oct-2015.

All of the below answers are given as effective 3 day rates.

"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.

Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:

Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:

A firm wishes to raise $50 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 6 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

A firm wishes to raise $50 million now. They will issue 5% pa semi-annual coupon bonds that will mature in 3 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

A firm wishes to raise $50 million now. They will issue 5% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

A 4.5% fixed coupon Australian Government bond was issued at par in mid-April 2009. Coupons are paid semi-annually in arrears in mid-April and mid-October each year. The face value is $1,000. The bond will mature in mid-April 2020, so the bond had an original tenor of 11 years.

Today is mid-September 2015 and similar bonds now yield 1.9% pa.

What is the bond's new price? Note: there are 10 semi-annual coupon payments remaining from now (mid-September 2015) until maturity (mid-April 2020); both yields are given as APR's compounding semi-annually; assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.

An investor bought a 5 year government bond with a 2% pa coupon rate at par. Coupons are paid semi-annually. The face value is $100.

Calculate the bond's new price 8 months later after yields have increased to 3% pa. Note that both yields are given as APR's compounding semi-annually. Assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.

Which of the following statements is NOT correct? Assume that all events are a surprise and that all other things remain equal. So for example, don't assume that just because a company's dividends and profit rise that its required return will also rise, assume the required return stays the same.

Refer to the below graph when answering the questions.

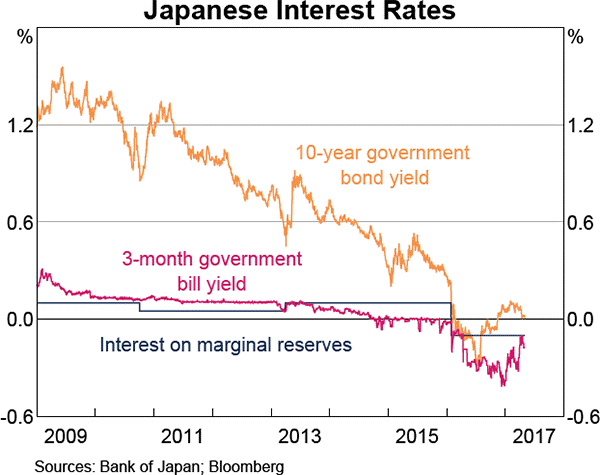
Which of the following statements is NOT correct?

Which of the following statements about vanilla floating coupon bonds is NOT correct? A vanilla floating coupon bond's:

Which of the following statements about vanilla floating coupon bonds paying quarterly coupons is NOT correct? A vanilla floating coupon bond's:

PIMCO gives the following example of an Inflation Linked Bond (ILB), called Treasury Inflation Protected Securities (TIPS) in the US.

How do ILBs work?

An ILB’s explicit link to a nationally-recognized inflation measure means that any increase in price levels directly translates into higher principal values. As a hypothetical example, consider a $1,000 20-year U.S. TIPS with a 2.5% coupon (1.25% on semiannual basis), and an inflation rate of 4%. The principal on the TIPS note will adjust upward on a daily basis to account for the 4% inflation rate. At maturity, the principal value will be $2,208 (4% per year, compounded semiannually). Additionally, while the coupon rate remains fixed at 2.5%, the dollar value of each interest payment will rise, as the coupon will be paid on the inflation-adjusted principal value. The first semiannual coupon of 1.25% paid on the inflation-adjusted principal of $1,020 is $12.75, while the final semiannual interest payment will be 1.25% of $2,208, which is $27.60.

Forecast the semi-annual coupon paid in 10 years based on the bond details given above. The 20th semi-annual coupon, paid in 10 years, is expected to be:

Read the below quote for background, or skip it to answer the question immediately.

In his 31 August 2021 article 'The rich get richer and rates get lower', Robert Armstrong states that:

"Atif Mian, Ludwig Straub and Amir Sufi agree with partisans of the demographic view, such as the economists Charles Goodhart and Manoj Pradhan, that a key contributor to falling rates is higher savings.

Mian, Straub and Sufi disagree, however, about why there are ever more savings sloshing around. It is not because the huge baby-boom generation is getting older and saving more (a trend that will change direction soon, when they are all retired). Rather, it’s because a larger and larger slice of national income is going to the top decile of earners. Because a person can only consume so much, the wealthy few tend to save much of this income rather than spend it. This pushes rates down directly, when those savings are invested, driving asset prices up and yields down; and indirectly, by sapping aggregate demand.

Why doesn’t all the cash that the rich push into markets get converted, ultimately, into productive investment, either at home or abroad? Tricky question. For present purposes it is enough to note that this is not happening — the savings of the American rich reappear, instead, as debt, owed by the government or by lower-income US households. (In another paper, MS&S have pointed out that this means the high share of income going to the rich hurts aggregate demand in two ways: the rich have a lower marginal propensity to consume, and governments and the non-rich are forced to shift dollars from consumption to debt service. Economically speaking, high inequality is a real buzzkill.)

MS&S prefer the inequality explanation for two reasons. Using data from the Fed’s Survey of Consumer Finances (which goes back to 1950) they show that differences in savings rates are much greater within any given age cohort than across age cohorts. That is, savings are building up faster because the rich are getting richer, not because the baby boomers are getting older."

Which of the following statements about this quote is NOT correct?

In the below chart by Rachel and Summers (2019), the red dotted line depicts the decline in advanced economies’ (AE) equilibrium real interest rate (R*) in percentage points since the 1970’s. The authors attribute this to the factors represented by columns above and below the x-axis. The sum of these columns is given by the black line labelled 'Total response of R* in the GE (general equilibrium) models'.

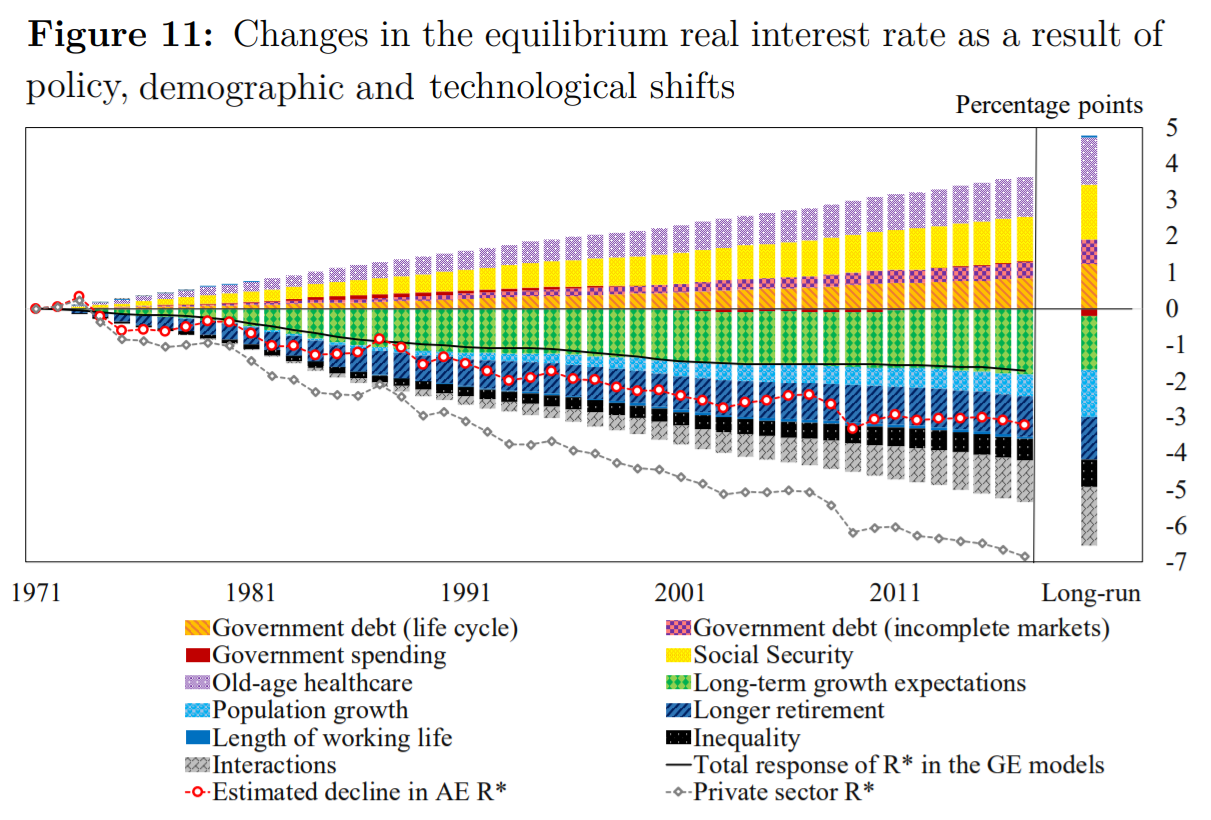
Which of the below statements about this graph is NOT correct?

In his 31 August 2021 article 'The rich get richer and rates get lower', Robert Armstrong states that: "Savings chase returns, so when there are more savings and the same number of places to put them, rates of return must fall" (Armstrong, 2021).

Another way of saying that "rates of return must fall" when there are more savings (loanable funds) invested into fixed coupon government and corporate bonds, is that increased:

An Australian government bond maturing in 10 years has a fixed coupon rate of 5% pa, paid semi-annually. The bond's yield-to-maturity (YTM) is currently 4% pa. The face value of the bond is $100. Which of the following statements is NOT correct?